Вектор
Наш девиз:
Задан вектор на удачу. Нам под силу все задачи.
Притча: «Вечность в бесконечности»
Однажды любопытный ученик, увидев в конце натурального ряда чисел три точки, спросил у своего учителя:
— Учитель, что же таится за этими тремя точками?
— За ними бесконечность, — ответил учитель.
— Что же это за число?
— Бесконечность – это число вечного движения.
— Так зачем же эти точки, почему бы просто не написать число?
— Эх, глупый, человек не может объять необъятное. Мы можем лишь представить, что там за ними.
— И что же, нам не суждено узнать, что там? Почему?
— Бесконечность есть то, что будет после нас, но мы знаем лишь то, что было до.
— Что же мы знаем?
— Мы знаем, что всё изнашивается, но человек совершенствуется и передаёт свои знания другим людям, как я тебе, но само развитие бесконечно. Бесконечность же недостижима, но мы можем прикоснуться к ней, оставив что-то этому миру, как однажды кто-то оставил нам эти три точки.
Глаза ученика загорелись, учитель продолжал:
— Как Пифагор оставил таблицу, как Евклид оставил теоретические тракты ,,Начала’’, как Ньютон оставил закон Всемирного тяготения или как Эйнштейн Теорию относительности. Все они давно умерли, но память об этих людях теперь вечна, а значит, они смогли прикоснуться к бесконечности.
Однажды любопытный ученик, увидев в конце натурального ряда чисел три точки, спросил у своего учителя:
— Учитель, что же таится за этими тремя точками?
— За ними бесконечность, — ответил учитель.
— Что же это за число?
— Бесконечность – это число вечного движения.
— Так зачем же эти точки, почему бы просто не написать число?
— Эх, глупый, человек не может объять необъятное. Мы можем лишь представить, что там за ними.
— И что же, нам не суждено узнать, что там? Почему?
— Бесконечность есть то, что будет после нас, но мы знаем лишь то, что было до.
— Что же мы знаем?
— Мы знаем, что всё изнашивается, но человек совершенствуется и передаёт свои знания другим людям, как я тебе, но само развитие бесконечно. Бесконечность же недостижима, но мы можем прикоснуться к ней, оставив что-то этому миру, как однажды кто-то оставил нам эти три точки.
Глаза ученика загорелись, учитель продолжал:
— Как Пифагор оставил таблицу, как Евклид оставил теоретические тракты ,,Начала’’, как Ньютон оставил закон Всемирного тяготения или как Эйнштейн Теорию относительности. Все они давно умерли, но память об этих людях теперь вечна, а значит, они смогли прикоснуться к бесконечности.

Бином Ньютона:
Почему формула бинома носит имя И. Ньютона?
Бином носит имя Исаака Ньютон, так как именно этот учёный, проведя большую работу, смог в 1665 году обобщить знания математиков Блеза Паскаля, Яна Хуэя, ат-Туси, аль-Каши, Штифеля, усовершенствовать их и вывести единую общую формулу для произвольного показателя степени двучлена. Именно он указал на возможность её разложения на случай и дробного, и отрицательного показателя.
Верно ли исторически название «Бином Ньютона»?
Исторически название «Бином Ньютона» верно, но лишь частично. Причиной этому является то, что вариации формулы Ньютона были известны ещё до рождения Ньютона. Их выводили и китайский математик Ян Хуэй, живший в XIII веке, и персидские математики ат-Туси (XIII век) и аль-Каши (XV век). В середине XVI века Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18. Более того Ньютоном не были приложены доказательства к своей формуле. Работу же закончил и дал строгое обоснование биному Н.Абель в 1826 году.
Почему в разных странах мира формулу бинома Ньютона называют по-разному? Укажите все названия, которые найдете.
Формулу называют по-разному. Есть такие вариации: формула бинома Ньютона, бином Ньютона, биноминальная формула Ньютона, формула общего члена бинома Ньютона.
По предложенной ниже ссылке вы можете увидеть карту, где собраны ученые, внесшие вклад в историю развития формулы Бинома Ньютона и самой теории.
https://padlet.com/araenius/gar4litevym37006
Бином Ньютона имеет применение в комбинаторике.
Пример 1
Найти число сочетаний множества, состоящего из четырех элементов: A, B, C, D по два

Действительно, это наборы (AB), (AC), (AD), (BC), (BD), (CD).
Пример 2
Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида (a+b)10a+b10. По условию имеем, что n=10, k=6−1=5n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента:

Бином Ньютона используется при решении задач по физике
Пример 1
Тяга воздушного винта и потребляемая им мощность вычисляются по формулам: P=apn2sD4N=bpn3sD5
Где D-диаметр винта; ns-число оборотов винта в секунду, p- плотность воздуха , a и b – коэффициенты зависящие от конструкции винта.
При ремонте винта для удаления с его концов царапин и зазубрин пришлось уменьшить его диаметр на величину ∆D, которая значительно меньше диаметра D.
Определить, на сколько снизилась тяга этого винта и потребляемая им Мощность при тех же секундных оборотах, если полагать все остальные параметры, входящие в формулы, неизменными.

Как это не удивительно, но Бином Ньютона упоминается даже в художественной литературе, когда речь идёт о чём-то очень сложном!
-
В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:
Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая карьера.
-
В романе «Мастер и Маргарита» М. А. Булгакова:
«подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
-
Позже это же выражение «Подумаешь, бином Ньютона!». упомянуто в фильме «Сталкер» А. А. Тарковского.
-
Роман Е. Н. Вильмонт получил название «Мимолетности, или Подумаешь, бином Ньютона!».
Треугольник Паскаля:

Самая ранняя сохранившаяся китайская иллюстрация « Треугольника Паскаля» взята из книги «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе 1303 года. Причем сам Чжу Шицзе называл этот треугольник «древним способом », не претендуя на роль первооткрывателя.
Цзя Сянь описал треугольник Паскаля (треугольник Цзя Сянь) примерно в середине 11 века, однако метод Цзя подробно изложил Ян Хуэй , который указал на свой источник: «Мой метод нахождения квадратных и кубических корней был основан на методе Цзя Сянь из Ши Суо Суан Шу».
Один из предшественников Омар Хайяма, аль-Караджи, уже открыл треугольное расположение коэффициентов биномиального разложения, которое европейцы позже узнали как треугольник Паскаля ; но Хайям распространил этот треугольный массив в Иране, и теперь он известен как треугольник Омара Хайяма.
Изображение Треугольника Паскаля, которое предоставил Омар Хайям.

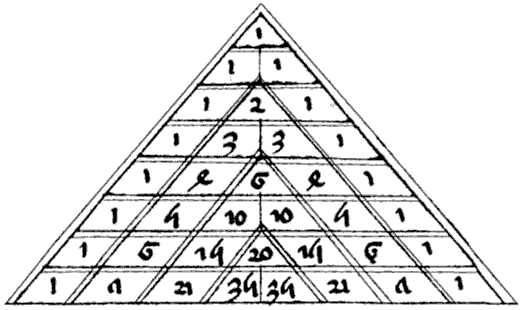
Современное изображение первых 14 строк треугольника Паскаля. Каждый элемент, не относящийся к боковой грани, равен сумме двух элементов, примыкающих к нему сверху – слева и справа
Нажав на данную ссылку, вы сможете рассмотреть ленту времени, основанную на более значимых событиях из жизни и научной деятельности Блеза Паскаля
Вы можете рассмотреть свойства треугольника Паскаля:
1.Числа треугольника симметричны относительно вертикальной оси
2.Первое и последнее числа равны 1
3.Третье число равно треугольному числу, что также равно сумме номеров предшествующих строк.
4.Второе и предпоследнее число равны n
5.Четвёртое число является тетраэдрическим
6.Сумма чисел n строки треугольника равна 2n
7.Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры
8.Все числа в n строке, кроме единиц делятся на число n, если n-простое число
9.Каждое число в треугольнике равно количеству способов добраться до него из вершины
Треугольник Серпинского:
1.Деятельность польского математика Вацлава Серпинского:
А) Вклад математика в развитие отдельных направлений математических наук:
Б) Термины, которые В. Серпинский ввел в современный математический понятийный аппарат:
1. Числа Серпинского:
2. Треугольник Серпинского:
3. Ковер Серпинского:
4. Кривая Серпинского:
5. Константа Серпинского.
6. Пространство Серпинского.



В) Объекты, в орнаменте которых можно выделить фракталы Серпинского:
1. Фракталы Серпинского можно разглядеть в строении сотовых антенн, такой вид строения позволяет уменьшить их размеры и вес. Фрактальные формы представляют собой симметрические фигуры относительно определенной точки:
2. Лук представляет собой незамысловатый фрактал, который состоит из колец разного диаметра:
3. Бутоны капусты сорта романеско похожи на все соцветие, каждый бутон состоит из таких же подобных бутонов, но меньших по размеру:
4. Снежинки также представляют фрактал, так как имеют сложное кристаллическое строение,а кристаллы в свою очередь идентичны между собой, поэтому снежинка имеет симметричную форму:




2.Построение "Треугольника Серпинского"
Построение таблицы:
1) записываем в первую строку и первый столбец единицы
2) начиная с В2 пишем формулу: =ОСТАТ(А2+В1;100) -> это сумма числа выше и ниже, но возьмем остаток деления на 100 (чтобы работало, так как получаются огромные числа)
3) заполняем так все ячейки (автозаполнением)
.png)
4) условное форматирование по формуле =ОСТАТ(А1;5)=0 - черный цвет
.png)
Вид получившегося треугольника Серпинского
.png)
Этот фрактал можно описать так:
Чтобы его получить, нужно взять прямоугольник с внутренностью.
Разбить его на 5х5 прямоугольников, всего 25 штук.
Провести в нём диагональ из нижнего левого угла в верхний правый угол. Закрасить нижний правый треугольник. Далее с десятью образовавшимися и оставшимися целыми маленькими прямоугольниками нужно сделать тоже самое. На рисунке показаны первые шаги.
Ссылка на скачивание фрактала:https://disk.yandex.ru/i/ufUoebTHMnqL4g